| MODIS Vegetation Indices (MOD13) C5 User’s Guide |
One of the primary interests of the Earth Observing System (EOS) program is to study the role of terrestrial vegetation in large-scale global processes with the goal of understanding how the Earth functions as a system. This requires an understanding of the global distribution of vegetation types as well as their biophysical and structural properties and spatial/temporal variations. Vegetation Indices (VI) are robust, empirical measures of vegetation activity at the land surface. They are designed to enhance the vegetation reflected signal from measured spectral responses by combining two (or more) wavebands, often in the red (0.6 - 0.7 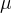 m) and NIR wavelengths (0.7-1.1
m) and NIR wavelengths (0.7-1.1 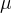 m) regions.
m) regions.
The MODIS VI products (MOD13) provide consistent, spatial and temporal comparisons of global vegetation conditions which can be used to monitor the Earth’s terrestrial photosynthetic vegetation activity in support of phenologic, change detection, and biophysical interpretations. Gridded vegetation index maps depicting spatial and temporal variations in vegetation activity are derived at 16-day and monthly intervals for precise seasonal and inter-annual monitoring of the Earth’s terrestrial vegetation.
Two VI products are made globally for land regions. The first product is the standard Normalized Difference Vegetation Index (NDVI), which is referred to as the continuity index to the existing NOAA-AVHRR derived NDVI. There is a +27-year NDVI global data set (1981 - 2009) from the NOAA-AVHRR series, which could be extended by MODIS data to provide a long term data record for use in operational monitoring studies. The second VI product is the Enhanced Vegetation Index (EVI), with improved sensitivity over high biomass regions and improved vegetation monitoring capability through a de-coupling of the canopy background signal and a reduction in atmosphere influences. The two VIs complement each other in global vegetation studies and improve upon the extraction of canopy biophysical parameters. A new compositing scheme that reduces angular, sun-target-sensor variations is also utilized. The gridded VI maps use MODIS surface reflectances corrected for molecular scattering, ozone absorption, and aerosols, as input to the VI equations. The gridded vegetation indices include quality assurance (QA) flags with statistical data that indicate the quality of the VI product and input data.
The MODIS VI products are currently produced at 250 m, 500 m, 1 km and 0.05 deg spatial resolutions. For production purposes, MODIS VIs are produced in tile units that are approximately 1200-by-1200 km, and mapped in the Sinusoidal (SIN) grid projection. Only tiles containing land features are processed, with the aim to reduce processing and disk space requirements. When mosaicked, all tiles cover the terrestrial Earth and the global MODIS-VI can thus be generated each 16 days and each calendar month.
The theoretical basis for empirical-based vegetation indices is derived from examination of typical spectral reflectance signatures of leaves. The reflected energy in the visible is very low as a result of high absorption by photosynthetically active pigments, with maximum absorption values in the blue (470 nm) and red (670 nm) wavelengths. Nearly all of the near-infrared radiation (NIR) is scattered (reflected and transmitted) with very little absorption, in a manner dependent upon the structural properties of a canopy (LAI, leaf angle distribution, leaf morphology). As a result, the contrast between red and near-infrared responses is a sensitive measure of vegetation amount, with maximum red NIR differences occurring over a full canopy and minimal contrast over targets with little or no vegetation. For low and medium amounts of vegetation, the contrast is a result of both red and NIR changes, while at higher amounts of vegetation, only the NIR contributes to increasing contrasts as the red band becomes saturated due to chlorophyll absorption.
NIR differences occurring over a full canopy and minimal contrast over targets with little or no vegetation. For low and medium amounts of vegetation, the contrast is a result of both red and NIR changes, while at higher amounts of vegetation, only the NIR contributes to increasing contrasts as the red band becomes saturated due to chlorophyll absorption.
The red-NIR contrast can be quantified through the use of ratios (NIR/red), differences (NIR red), weighted differences (NIR
red), weighted differences (NIR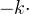 red), linear band combinations (
red), linear band combinations (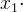 red
red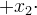 NIR), or hybrid approaches of the above. Vegetation indexes are measures of this contrast and thus are integrative functions of canopy structural (%cover, LAI, LAD) and physiological (pigments, photosynthesis) parameters.
NIR), or hybrid approaches of the above. Vegetation indexes are measures of this contrast and thus are integrative functions of canopy structural (%cover, LAI, LAD) and physiological (pigments, photosynthesis) parameters.
The NDVI is a normalized transform of the NIR to red reflectance ratio, 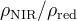 , designed to standardize VI values to between
, designed to standardize VI values to between 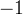 and
and 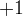 . It is commonly expressed as:
. It is commonly expressed as:
 |
(1) |
As a ratio, the NDVI has the advantage of minimizing certain types of band-correlated noise (positively-correlated) and influences attributed to variations in direct/diffuse irradiance, clouds and cloud shadows, sun and view angles, topography, and atmospheric attenuation. Ratioing can also reduce, to a certain extent, calibration and instrument-related errors. The extent to which ratioing can reduce noise is dependent upon the correlation of noise between red and NIR responses and the degree to which the surface exhibits Lambertian behavior.
The main disadvantage of ratio-based indices tend to be their non-linearities exhibiting asymptotic behaviors, which lead to insensitivities to vegetation variations over certain land cover conditions. Ratios also fail to account for the spectral dependencies of additive atmospheric (path radiance) effects, canopy-background interactions, and canopy bidirectional reflectance anisotropies, particularly those associated with canopy shadowing.
A major finding on atmospheric effect minimization is the use of the difference in blue and red reflectances as an estimator of the atmosphere influence level. This concept is based on the wavelength dependency of aerosol scattering cross sections. In general the scattering cross section in the blue band is larger than that in the red band. When the aerosol concentration is higher, the difference in the two bands becomes larger. This information is used to stabilize the index value against variations in aerosol concentration levels.
The EVI incorporates this atmospheric resistance concept as in the Atmospheric Resistant Index (ARVI), along with the removal of soil-brightness induced variations in VI as in the Soil Adjusted Vegetation Index (SAVI). The EVI additionally decouples the soil and atmospheric influences from the vegetation signal by including a feedback term for simultaneous correction. The EVI formula is written as:
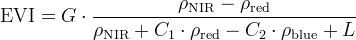 |
(2) |
where 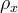 are the full or partially atmospheric-corrected (for Rayleigh scattering and ozone absorption) surface reflectances;
are the full or partially atmospheric-corrected (for Rayleigh scattering and ozone absorption) surface reflectances; 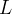 is the canopy background adjustment for correcting nonlinear, differential NIR and red radiant transfer through a canopy;
is the canopy background adjustment for correcting nonlinear, differential NIR and red radiant transfer through a canopy; 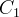 and
and  are the coefficients of the aerosol resistance term (which uses the blue band to correct for aerosol influences in the red band); and
are the coefficients of the aerosol resistance term (which uses the blue band to correct for aerosol influences in the red band); and 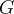 is a gain or scaling factor. The coefficients adopted in the EVI algorithm are,
is a gain or scaling factor. The coefficients adopted in the EVI algorithm are, 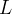 =1,
=1, 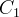 =6,
=6,  =7.5, and
=7.5, and 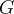 =2.5.
=2.5.
The EVI is replaced by a modified 2-band EVI (which does not use the blue band) over high-reflectance surfaces such as clouds and snow/ice. This backup method is used to avoid an atmospheric over-correction condition by EVI, caused by a high blue band reflectance over those surfaces. This situation may be exacerbated by an imperfect atmospheric correction procedure, which would promote further anomalous EVI values. Because the 2-band EVI lacks the blue band, it becomes insensitive to these effects, while maintaining the other advantages of the EVI.
The 2-band EVI equation used for the MODIS VI products is:
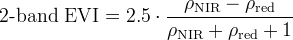 |
(3) |
Prior to Collection 5, the SAVI algorithm was used as the EVI backup algorithm for the MODIS VI Products.
Please refer to the “MODIS Vegetation Index (MOD 13) Algorithm Theoretical Basis” document (http://modis.gsfc.nasa.gov/data/atbd/atbd_mod13.pdf) for an in-depth review of the MODIS VI scientific basis.